CS149 Lab Report
Lab1
第一个实验主要让学生体验并行计算的优势(多线程,SIMD,ispc),要写的代码不多。
Prog1
本实验用多线程计算Mandelbrot Set,并与单线程进行性能比较。对于Mandelbrot Set,我们需要知道的是:
- 每个像素的计算是独立进行的,和其他像素无关。
- 不同像素的计算代价不一样。从图上看,越亮的点计算代价越大。
因此,问题的关键在于如何把计算任务分配给各线程。
最直接的想法是把整个区域横向平均分割成\(n\)块,每个线程按顺序取自己的一部分进行计算。从图1可以看出,中间部分的亮点数量更多,因此需要的计算代价也更大。因此线程号在中间的线程需要更长时间完成任务,成为性能瓶颈。
一种改进方法是让两侧的线程处理更多的行,中间的线程处理更少的行。但是如何取不同分割比例不是一个简单问题,而且不适用于图2。
因此,我让线程\(i\)处理$Row% n == i
$的那些行,这样做实现简单,需要修改一下mandelbrotSerial函数。
测试结果
测试在i7-12700平台(8P4E)上进行,用taskset绑定到8个大核。
Naive实现:
| 线程数 | view1 | view2 |
|---|---|---|
| 1 | 1.00 | 1.00 |
| 2 | 1.95 | 1.66 |
| 3 | 1.62 | 2.13 |
| 4 | 2.39 | 2.51 |
| 5 | 2.42 | 2.84 |
| 6 | 3.17 | 3.23 |
| 7 | 3.30 | 3.61 |
| 8 | 3.90 | 4.00 |
Step实现:
| 线程数 | view1 | view2 |
|---|---|---|
| 1 | 0.99 | 0.99 |
| 2 | 1.95 | 1.94 |
| 3 | 2.86 | 2.84 |
| 4 | 3.81 | 3.78 |
| 5 | 4.66 | 4.63 |
| 6 | 5.58 | 5.51 |
| 7 | 6.35 | 6.31 |
| 8 | 7.27 | 7.20 |
继续增加线程数对性能提升没有帮助,因为只有8个核。
Prog2
本实验旨在介绍SIMD指令的使用方式,需要使用框架提供的“模拟”SIMD指令完成一些功能。
clampedExpVector
该函数需要计算\(\max (9.999999, value[i] ^
{exp[i]})\),由于每个分量的结果只和该分量的参数有关,不涉及不同分量之间的运算,因此只需要用SIMD指令模拟一下串行执行的逻辑即可。框架已经给出了一个absVector作为示例。
注意正确使用mask,为了处理VECTOR_WIDTH不能整除N的情况,应该用_cs149_init_ones(min(VECTOR_WIDTH, *N* - i))来设置全局的mask。示例代码absVector不能处理这种情况,也是因为这个原因。
arraySumVector
该函数需要计算\(\sum\nolimits_{i=0}^NV_i\),这个函数的串行实现非常直接,但是使用SIMD进行计算的逻辑却完全不同,因为涉及到不同分量之间的运算。
做法是用hdd指令把相邻的分量加到一起,再用interleave指令把结果换到一起,再用hdd指令累加,重复这个过程直到得到最终结果,类似于一个归并过程。
这里假设了VECTOR_WIDTH是2的幂次,且N能被VECTOR_WIDTH整除。
测试结果
测试\(N=10000\)时,改变SIMD指令操作的向量宽度,向量利用率的变化情况。向量利用率越低,说明运算过程中有越多的分量被mask屏蔽而没有参与计算。
| 向量宽度 | 向量利用率 |
|---|---|
| 2 | 86.4% |
| 4 | 81.8% |
| 8 | 79.4% |
| 16 | 78.2% |
| 32 | 77.7% |
| 64 | 77.5% |
| 128 | 77.1% |
| 256 | 76.5% |
可以看出,向量宽度越高,利用率也越低,因为高维向量意味着处理一个进入了不同分支的分量会阻塞更多的分量。
Prog3
本实验主要分析ispc程序的性能。ispc会使用SIMD指令加速执行(仍然是单核),ispc task还会启动多个task(类似于线程),跑在多个核上。
由于ispc使用宽度为8的AVX2指令,我们期望的理想性能提升是8倍,实际上只有2-4倍,这还是因为不同像素的计算开销不同导致的。和实验1不同的是,simd指令处理的向量对应到一组邻近的像素点,因此如果白点分布的比较离散,一个白点就会拖慢周围的其他黑点。因此图2比图1的提升幅度还要少一点。
在使用了ispc task后,我观测到task数目为16时性能提升达到峰值。这个行为有些奇怪,因为物理核数是8。
Prog4
本实验以牛顿迭代法求平方根为例,分析SIMD的best/worst case。在baseline中,需要开方的输入数组是随机生成的。
对于best case,把所有输入置为2.99999,因为接近3的数迭代次数最多,计算代价最大,SIMD最能体现出针对串行程序的优势。此外,整个输入数组相同意味着控制流不会进入不同分支,屏蔽了SIMD的劣势。
对于worst case:
- 思路1:所有输入置为1,此时只需要1次迭代,瓶颈不在计算而在访存上,SIMD优势不明显。
- 思路2:对于每组8个输入,设置其中1个为2.99999,其他都设为1。此时SIMD的执行速度被拖慢到对2.99999开方的速度,因此可能比串行还要慢。
测试结果
| 测试 | ISPC提升比例 | 带task的ISPC提升比例 |
|---|---|---|
| baseline | 3.77 | 30.49 |
| best | 5.15 | 37.92 |
| worst1 | 1.38 | 1.96 |
| worst2 | 0.89 | 6.67 |
Prog5
本实验分析SIMD对于一个简单计算任务的性能提升。在这个场景中,ispc几乎没有任何提升,而ispc task的提升也只有1.2倍左右,因为此时的瓶颈在内存读取上。
在计算访存次数时,框架认为每个元素对应4次访存操作。这是因为除了读取两个原数据以外,写回时会带来2次访存操作:
- write-back:cache未命中时,将需要修改的数据复制到cache,修改cache中的数据。写回时会带来另一次内存访问,共两次。
- write-through:cache未命中时,直接写入内存,同时将修改后的数据读进cache,也是两次。
Prog4 Extra
本实验要求自己用SIMD指令实现一个浮点数开方运算。Intel为AVX指令集提供了一系列内置函数,编程者不需要手写汇编。
虽然实验要求用AVX2指令集进行实现,但似乎AVX2涉及的大部分是整型数运算,我用到的函数都来自AVX.
实现中,我模仿了标量运算的牛顿迭代法,用到的都是比较基本的AVX函数。
一些注意点:
- AVX内置的算术运算函数不像proj2中的那些函数一样,有一个mask参数,因此分支操作比较麻烦,要依赖
_mm256_blendv_ps(也可能是我没找到正确用法)。 - 比较操作
_mm256_cmp_ps的第三个参数,可以参考这里。我使用的是ordered, non-signaling的版本。 - 我使用的都是宽度为256位的AVX函数,即同时处理8个单精度浮点数。
测试结果
我的实现性能比不上ispc,AVX内置的开方函数_mm256_sqrt_ps性能远胜ispc.
| 测试 | 执行时间/ms | 提升比例 |
|---|---|---|
| serial | 1658.965 | 1x |
| ispc | 428.850 | 3.87x |
| ispc task | 58.057 | 28.57x |
| my AVX | 686.149 | 2.42x |
| AVX native | 19.576 | 84.75x |
Lab2
第二个实验要求实现一个并行执行任务的c++库,以充分利用多核性能。
Part A
A部分会实现同步执行任务的语义,即用户通过ITaskSystem::run(IRunnable* runnable, int num_total_tasks)指定一个可执行对象runnable,task
system会执行该对象的num_total_tasks个实例,并在这些实例都执行完成后同步地从run()返回。
具体来说,实验要求了3种实现:
TaskSystemParallelSpawn,每次调用run()时创建线程来执行task,run()返回时销毁线程。TaskSystemParallelThreadPoolSpinning,task system初始化时创建线程池执行task,空闲时这些线程自旋等待。TaskSystemParallelThreadPoolSleeping,同上,但是空闲时这些线程进入睡眠。
TaskSystemParallelSpawn
流程:
- 每次调用
run()时,通过std::thread()创建新线程,并在参数中传入一个全局计数器。 - 每个worker线程会fetch-and-add该计数器的值。如果取到的值是合法的task index则执行任务,否则该线程结束运行。
run()返回前通过join()操作等待所有worker线程结束运行。
以上流程是动态将任务分配给进程的。第2步的fetch-and-add可以通过互斥锁实现,也可以更方便地使用std::atomic。
TaskSystemParallelThreadPoolSpinning
流程:
- 在TaskSystem的构造函数中创建线程池。
- 每个worker线程执行一个无限循环,试图通过fetch-and-add获取当前task index。如果合法则执行任务,否则继续自旋等待。
- 每个worker线程执行完任务后,需要原子递增一个计数器
_done_cnt。 run()会在设置好有关状态后自旋等待,直到_done_cnt == num_total_tasks。- TaskSystem的析构函数需要让所有worker线程退出循环,并使用
join()等待它们结束运行。
主线程会在第4步中设置一些状态,worker线程会读取这些状态;类似地,worker线程设置_done_cnt,并由主线程读取。对这些状态的读写需要拿互斥锁以保证原子性。
std::atomic
我尝试通过std::atomic修改状态,但是不能保证正确性。因为有些状态的修改涉及多个原子变量,std::atomic只能保证对单个变量的修改是原子的。比如我的实现是:
1 | void TaskSystemParallelThreadPoolSpinningAtomic::thread_task() { |
考虑run()被连续调用两次,且num_total_tasks分别为3和100。在第一次调用中,_doing_cnt可能被worker线程在第8行中增加到一个\(\ge
3\)的值。当然,只有小于3的值是合法的task index并被执行。
如果一个worker线程执行完第8行,读到index=50并被调度走。第一次调用完成后紧接着第二次调用,主线程在21行将_ntask修改为100,此时上述worker线程恢复运行。它会通过第10行的检查,并执行task
index为50的任务。这种行为是错误的,因为index是一个上一轮run()调用中遗留下来的值。
这种情况出现的本质原因是index变量存在一个TOCTOU的问题,要通过互斥锁防止该变量在”读取之后,比较之前“被修改。
TaskSystemParallelThreadPoolSleeping
流程:
- 在TaskSystem的构造函数中创建线程池。
- 每个worker线程执行一个无限循环,试图通过fetch-and-add获取当前task index。如果合法则执行任务,否则进入睡眠。
- 每个worker线程执行完任务后,原子递增
_done_cnt。如果_done_cnt == _ntask则唤醒主线程。 run()在设置好状态后进入睡眠,等待被worker线程唤醒。- TaskSystem的析构函数需要让所有worker线程退出循环(可能还需要唤醒它们),并使用
join()等待它们结束运行。
睡眠和唤醒可以通过条件变量实现。主线程和worker线程都需要用互斥锁保护,worker线程只在实际执行任务时放锁,执行完了重新拿锁。
一些注意点:
- 析构时,主线程需要保证所有worker线程都能退出循环,因此析构函数也必须获取互斥锁。否则主线程可能在某些worker线程即将进入睡眠之前调用
notify_all(),导致这些worker线程睡眠后永远无法被唤醒。 - 在每轮循环中,worker线程的临界区开始于任务执行完成时,终止于即将执行任务时。因此worker线程不能在每轮循环的起始处拿锁,结束处放锁,而是在循环外面拿锁,在
runTask()前后分别进行unlock()和lock()操作。
Part B
本部分实现异步执行的语义,同时引入dependency的概念。ITaskSystem::runAsyncWithDeps(IRunnable* runnable, int num_total_tasks, const std::vector<TaskID>& deps会立刻返回,无需等待任务完成。同时该任务与一个deps关联,只有该数组中所有任务都已完成后,当前任务才能被执行。ITaskSystem::sync()会在当前存在的所有任务执行完成后返回。
以下将每次run()或者runAsyncWithDeps()中指定的任务称为bulk,每个bulk中包含num_total_tasks个task。
本实验只实现TaskSystemParallelThreadPoolSleeping。与Part
A的区别在于:
- task system中可能有多个bulk等待执行,若bulk中task数目少于worker线程数,多个bulk需要同时被执行。
- 需要处理bulk之间的依赖问题。
因此我的做法是:
- 将
_doing_cnt_done_cnt等变量变为per bulk的元数据,将每个bulk的元数据存入一个队列。worker线程发现某个bulk中的所有task都已经/正在被执行后,会寻找队列中的下一个bulk并执行,找不到则进入睡眠。执行每个bulk中最后一个task的worker线程需要将该bulk的元数据从队列中移除。 - 将新创建的bulk加入等待队列,并维护已经完成的bulk集合。每当有bulk完成时,检查是否有等待队列中bulk可以被执行,并将其移入执行队列。这样做会有越来越高的内存占用,但对实验中的测试用例是足够的。
性能
在我的测试中,所有用例单独运行时都能满足性能要求,但是由run_test_harness.py一起运行时不能保证全部通过。此外,用例的执行时间在多次运行时波动较大。
Lab3
Lab3是一个使用CUDA的实验。
Part A
本部分需要补全CUDA版本的saxpy程序并计时,只需要补充其中有关显存的代码。
测试结果可以看出,saxpy程序中,在CPU和GPU之间拷贝数据的开销远大于GPU执行计算的开销。
1 | Effective BW by CUDA saxpy: 387.895 ms (kernel: 17.200 ms) [2.881 GB/s] |
Part B
本部分实现一个并行的find_repeaet算法,返回数组中A满足\(A[i] = A[i+1]\)的下标\(i\)。
exclusive scan
文档提示,通过课件中介绍的exclusive scan算法来实现find_repeat。因此首先要实现work-efficient exclusive scan的并行版,串行版本如下:
1 | void exclusive_scan_iterative(int* start, int* end, int* output) { |
只需要做简单的伪代码翻译,把parallel_for的部分替换为cuda
kernel调用即可,即每次parallel_for会启动N个cuda线程,每个线程判断自己的下标\(idx\)是否满足idx % two_dplus1 == 0,如果是则执行循环体内的操作。
一种优化的实现是在每轮循环中不开N个线程,只开对应数目的线程执行循环体中的操作,在线程中就不用判断下标了。这样做需要控制最后一个thread
block中的线程数目,不能简单地开满THREAD_PER_BLOCK个,编程复杂度更高。因此我没有采用这种做法。
find repeat
基于exclusive scan可以实现find
repeat,流程如下,以A={1, 2, 2, 1, 1, 1, 3, 5, 3, 3}为例:
- 计算数组B,标记满足
A[i] == A[i+1]的元素,赋值为1,否则赋值0,得到B = {0, 1, 0, 1, 1, 0, 0, 0, 1, 0}。 - 对数组B计算exclusive
scan,得到
C = {0, 0, 1, 1, 2, 3, 3, 3, 3, 4}。 - 再次判断\(A[i] ==
A[i+1]\),令
output[c[i]] = i。 - 重复元素的数目可以从数组C的最后一个元素获得。
PartC
PartC要求实现一个并行版本的圆形渲染算法。在框架提供的CUDA实现中,每个CUDA线程负责渲染一个圆,更新其覆盖的每个像素的颜色。这样做不能保证:
- 原子性。每个像素的属性由RGBA四个值表示,对它们的更新必须是原子的,不能只更新一半。
- 更新顺序,像素颜色的更新不具备交换性。如果多个圆覆盖了同一个像素,对该像素的更新必须严格按照圆的顺序进行。
然而,如果每个像素的属性由且仅由一个CUDA线程进行更新,就可以轻而易举地满足这些要求。因此,我们为图片中每个像素分配一个CUDA线程,并在kernel函数中遍历所有的圆,判断当前像素是否在圆中并更新颜色即可。
1 | __global__ void kernelRenderPixels() { |
从实验描述看来,这是一个相当复杂的实验。因此这个做法应该不是实验设计者所期望的,不过性能确实远远优于参考实现。
Lab4
Lab4是一个使用OpenMP的实验。
PartA
本部分利用openMP实现一个基础的pagerank算法。框架给出了伪代码,只需要翻译成单线程版的代码,再用#pragma omp parallel for修饰for循环即可,需要注意:
- 操作并发不安全的数据结构(如
std::vector)的for循环不能并行。 - 遍历图中每个节点是相互独立的,可以并行。
- 遍历每个节点的所有入边的for循环如果并行,会导致性能很差。根据这里,嵌套两层
#pragma omp parallel for时,第二层是无效的,并不会创建更多子线程来执行第二层循环,同时还会引入额外的overhead。
PartB
本部分实现传统的,自上而下的BFS算法的并行版本。除了使用OpenMP对for循环并行化以外,还需要进行其他优化才能达到参考性能。参考了wangdh15的实现,还需要做:
- 通过CAS操作修改
distances[node],确保只有每个新节点只被一个线程加入new_frontier数组。(测试表明,即使节点被重复加入,性能也不会受到很大影响) - 每个线程只写入自己的局部
new_frontier数组,循环结束后再合并到全局new_frontier中去。
PartC
本部分实现自下而上的BFS,伪代码如下:
1 | for each vertex v in graph: |
在实现中并不需要维护frontier,通过判断节点u的距离是否等于BFS的深度,即可得知节点u是否属于frontier。看起来除了#pragma omp parallel for也没有其他的优化点。即便如此,Part
C的参考实现快的离谱,我的实现也无法获得全部分数。
PartD
Part D要求混合B和C两部分的实现来优化BFS性能,方法也十分显然:自上而下和自下而上的BFS分别适用于frontier中节点较少和较多的情形。因此根据frontier中节点数目占图中总节点数的比例(我使用了10%),来判断每一步搜索应采用自上而下/自下而上的BFS即可。
Extra
在最后一个实验中,我简单用AVX指令实现了GEMM(General matrix multiply)。AVX指令为256位,矩阵元素为双精度浮点数,因此一条avx指令可以操作4个元素。
在朴素的想法中,我们将矩阵A的第\(i\)行和矩阵B的第\(j\)列作为向量相乘,得到矩阵C的\((i, j)\)元素,如下图。
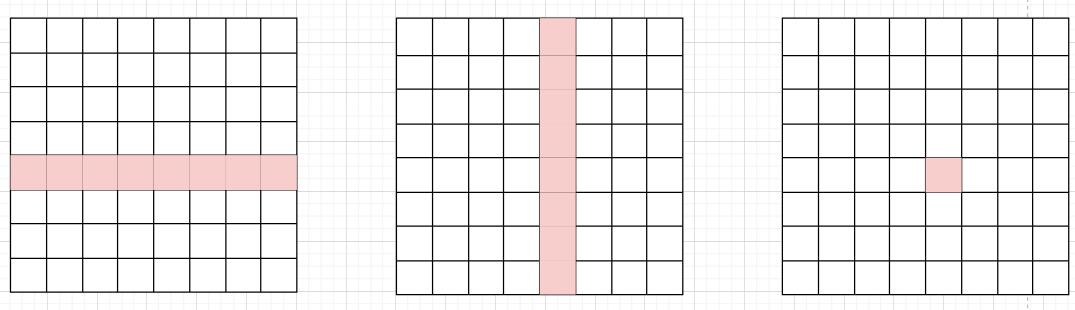 这样做是没法利用AVX指令的,因为矩阵B的那一列在内存中并不连续存储。正确做法是把矩阵B中的相邻\(n\)列联合起来考虑,如下图。其中\(n\)为avx指令能够同时操作的矩阵元素数目,这里为4。
这样做是没法利用AVX指令的,因为矩阵B的那一列在内存中并不连续存储。正确做法是把矩阵B中的相邻\(n\)列联合起来考虑,如下图。其中\(n\)为avx指令能够同时操作的矩阵元素数目,这里为4。
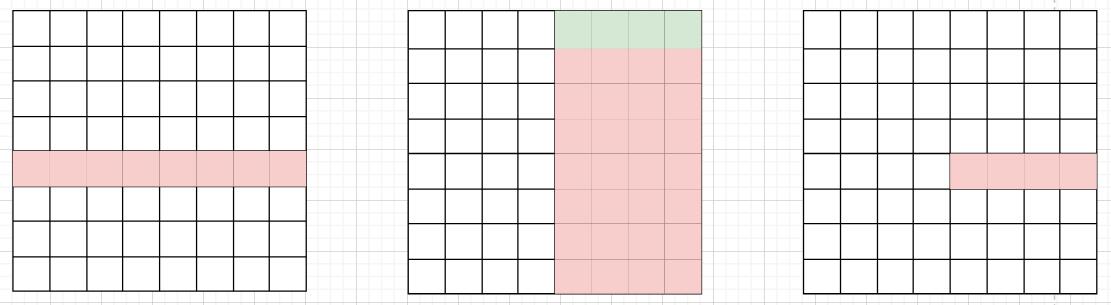
这样一来,我们就可以对绿色标出的,同行不同列的元素使用AVX指令,一次性计算出矩阵C中的4个元素。
我的实现性能大约是ISPC参考实现的三分之一。